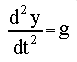|
For the first demonstration of the Euler method, we will look at
an object falling in a constant gravitational acceleration field:
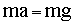
This leads to
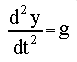
As mentioned earlier, we can convert this second order equation
to two first order equations by substituting the velocity variable.
The Euler formula for the velocity is then
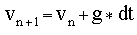
and the vertical coordinate formula becomes
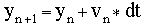
The Falling Object demo program below shows the results of these
formulas for four values of dt.
It also compares the results to the analytical formulas. (We provide
the code for both an applet and an application.)
FallingObject_Applet1.java
(Output goes to browser's Java
console.) |
|
public
class
FallingObject_Applet1 extends
java.applet.Applet
{
public
void init()
{
// Put code
between this line
//--------------------------------------------------
double
t, y, vy;
double
total_t;
int
n;
// Constants
double
y0 = 0.0;
double
v0 = 0.0;
double
g = -9.80;// meter per sec**2
// Version
1
double
dt = 0.1;
int
n_steps = 10;
y = y0;
vy = v0;
for(n=0;
n < n_steps; n++)
{
y = y + vy * dt;
vy = vy + g *
dt;
}
total_t = n * dt;
System.out.println("Version
1, dt=0.1 ");
System.out.println("Time =
" + total_t);
System.out.println("y = "
+ y + ", vy = " + vy);
System.out.println();
// Version
2
dt = 0.01;
n_steps = 100;
y = y0;
vy = v0;
for(
n=0; n< n_steps; n++)
{
y = y + vy * dt;
vy = vy + g *
dt;
}
total_t = n * dt;
System.out.println("Version
2, dt=0.01 ");
System.out.println("Time =
" + total_t);
System.out.println("y = "
+ y + ", vy = " + vy);
System.out.println();
// Version
3
dt = 0.001;
n_steps = 1000;
y = y0;
vy = v0;
for(
n=0; n < n_steps; n++)
{
y = y + vy * dt;
vy = vy + g *
dt;
}
total_t = n * dt;
System.out.println("Version
3, dt=0.001 ");
System.out.println("Time =
" + total_t);
System.out.println("y = "
+ y + ", vy = " + vy);
System.out.println();
// Version
4
dt = 0.0001;
n_steps = 10000;
y = y0;
vy = v0;
for(
n=0; n< n_steps; n++)
{
y = y + vy * dt;
vy = vy + g *
dt;
}
total_t = n * dt;
System.out.println("Version
4, dt=0.0001 ");
System.out.println("Time =
" + total_t);
System.out.println("y = "
+ y + ", vy = " + vy);
System.out.println();
vy = v0 + g;
y = y0 + 0.5 * g;
System.out.println("Formulas
for Total time = 1.0sec");
System.out.println("y = "
+ y + ", vy = " + vy);
//--------------------------------------------------
//
and this line.
}
//
Paint message in Applet window.
public void paint(java.awt.Graphics
g)
{ g.drawString("FallingObject_app1",10,20);
}
}
|
|
|
The output of the program goes as follows:
Version
1, dt=0.1
Time = 1.0
y = -4.410000000000001, vy = -9.800000000000002
Version 2, dt=0.01
Time = 1.0
y = -4.850999999999997, vy = -9.800000000000006
Version 3, dt=0.001
Time = 1.0
y = -4.895100000000021, vy = -9.800000000000114
Version 4, dt=0.0001
Time = 1.0
y = -4.899510000000613, vy = -9.800000000001582
Formulas for tTotal = 1.0sec
y = -4.9, vy = -9.8 |
Note: The long fractions in
the decimal values is rather annoying but we will wait till Chapter
5: Tech to discuss how to specify the format of numbers in the
print output .
We see that the y
drop distance varies according to the choice of dt.
The finer the increment, the closer the distance matches the analytical
result.
The discrepencies between the Euler method and the analytical formula
come from three sources:
- Truncation error - Our choice
of dt
in the algorithm leads to a particular level of error. This error
would occur no matter what language or processor we used. This
algorithm dependent error is usually referred to in numerical
methods literature as the truncation error.
Here the computation of y
assumes that the velocity remains constant during dt,
which is not true, though as dt
becomes smaller and smaller, the error becomes smaller as well.
- Computation error - The
variation in the higher digits comes from our choice (or the processor
designer's choice) of the floating point precision. A floating
point type with an infinitely wide mantissa would eliminate such
error entirely but for real world computers, this error is unavoidable
at some level of precison.
Exercise: Modify the above
demo program to use float
types instead of double.
Note that you will need to change the floating point literals to
float types
as well by appending 'f', e.g. g
= -9.80f.
Can you see changes in the results due to the lower precision float
type? Try letting it fall further, e.g. larger nSteps,
to see if the discrepancies grow.
Latest update: Oct. 22, 2005
|