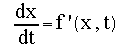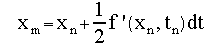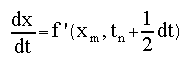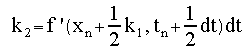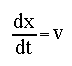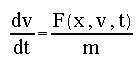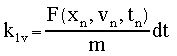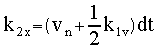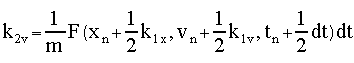Introduction
Inheritance
  Demo 1
Overriding
  Demo 2a   Demo 2b
this,super
MoreConstructors
  Demo 3
Abstraction
Interface 
  Demo 4
Casting References
MoreAboutArrays
Object class
Class Summary
Exercises

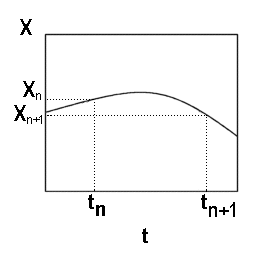
The diagram below shows the true trajectory of our ODE and the points separate by dt.

The Euler method is an asymmetric method since it uses only information on the nth point, or the "left" point, to find the position and derivative (for example, the velocity in the equation of motion example) at the n+1 point, or right point.

The Predictor-Corrector method does somewhat better by using an average of the function value at the n and (predicted) n+1 points to get a better estimate of the new derivative.

Note also that these are first-order methods in the dependent variable dt.

There are a number of improved methods that attempt to take a more symmetric approach. In particular, they make a better estimate of the slope at the midpoint between t_n and t_(n+1).

We will concentrate here on midpoint method that is also 2nd order in dt.

We begin with a first oder ODE:

For a dt interval we can obtain an estimate at the midpoint position with the Euler method:

Then, in turn, use this to obtain the midpoint slope

We can use this midpoint slope to estimate the position across the full interval.. This approach is usually expressed in such a way that the final formula looks similar to the Euler formula by giving names to the intermediate terms (using k by convention):

This set of equations is referred to as the midpoint or second-order Runge-Kutta method.

Note that this approach is symmetric over the dt segment and the term k₂ is second order in dt.

As discussed earlier, we usually will need to solve a set of such equations. For the equation of motion we need to solve for both the position and the velocity of an object responding to a force F(x,v,t) :

then

            Tech
MoreComplexClass
ImprovedHistogram
JavaRandomNums
Vectors & Matrices
Exercises

           Physics
Runge-Kutta 2nd
  Demo 1
Runge-Kutta 4th
  Demo 2
BoundaryVal.Prob
Shooting Method
  Demo 3
Exercises