
| Home : Map : Chapter 5 : Java : Tech : Physics : |
|
Integration Methods
|
| JavaTech |
| Course Map |
| Chapter 5 |
|
File/Package/Import Demo 1 Demo 2 Access/Visibility final & Constants Static Import Jar Files Demo 3 Applet Directories 3rd Party Packages CLASSPATH javadoc CodingConventions Exercises |
|
Supplements
|
| About
JavaTech Codes List Exercises Feedback References Resources Tips Topic Index Course Guide What's New |
Integration of functions is a common task in numerical analysis. In this chaper we look at some basic techniques.
As found in your calculus book, the integral of function f(x)
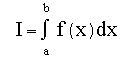
can be approximated by the summation of the areas of slices, or rectangles, beneath the function
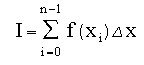
where
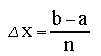
and ![]() goes
to zero as n goes to infinity.
goes
to zero as n goes to infinity.
This approximation can certainly be used for numerical integration but it will not provide very accurate values for most functions of interest. The flat top of the rectangle will not match well with curving functions and this error will accumulate for practical values for n. As n increases, eventually the accumulation of round off errors becomes the dominant error.
If we approximate the function over the dx interval with the linear interpolation formula:
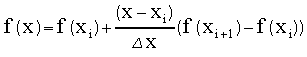
then for a fixed ![]() we obtain
we obtain
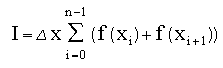
or
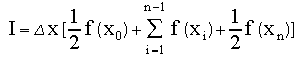
This is called the trapezoid rule as the sum is over the areas of trapezoids with sides of heights f(xi) and f(xi+1)and width delx.
References & Web Resources
|
Tech |
|
Physics |